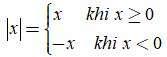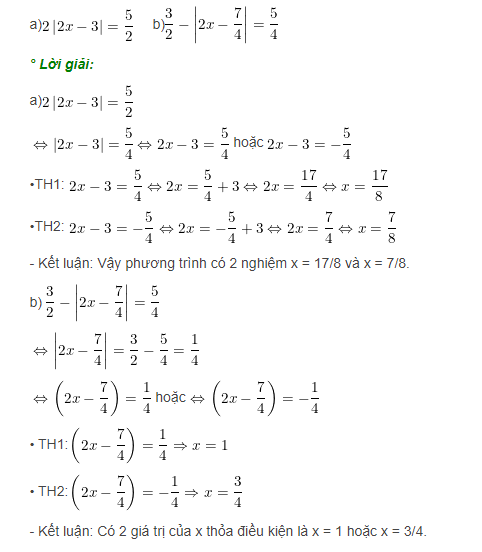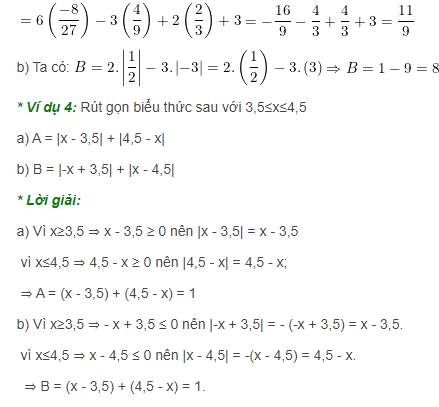Giá trị tuyệt đối là kiến thức cơ bản được học từ trung học cơ sở nhưng có rất nhiều các bạn học sinh không nắm vững được giá trị tuyệt đối, dấu giá trị tuyệt đối, tính chất giá trị tuyệt đối, phương trình chứa dấu giá trị tuyệt đối, bất phương trình chứa dấu giá trị tuyệt đối và các phương pháp giải giá trị tuyệt đối như thế nào? Sau đây, chúng tôi sẽ chia sẻ lý thuyết giá trị tuyệt đối là gì và các dạng bài tập liên quan nhé
Giá trị tuyệt đối là gì?
Giá trị tuyệt đối của số hữu tỉ x, kí hiệu là|x|,là khoảng cách từ điểm x tới điểm 0 trên trục số.
Đang xem: Cách tính trị tuyệt đối
Nếu x > 0 thì |x| = x.Nếu x = 0 thì |x| = 0.Nếu x
Từ định nghĩa trên ta có thể viết như sau:
Ví dụ:
Nếu
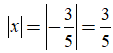
Nếu x = 6 thì |x| = |6| = 6.
Chú ý: Với mọi x ∈ Q ta luôn có |x| ≥ 0, |x| = |-x|, |x| > x.
Tính chất của giá trị tuyệt đối
Giá trị tuyệt đối của số không âm là chính nó, giá trị tuyệt đối của số âm là số đối của nó.
Nếu a ≥ 0 => |a| = aNếu a |a| = -aNếu x – a ≥ 0 => |x – a| = x – aNếu x – a ≤ 0 => |x – a| = a – x
Giá trị tuyệt đối của mọi số đều không âm |a| ≥ 0 với mọi a ∈ R. Cụ thể:
|a| =0 a = 0|a| ≠0 a ≠0
Hai số bằng nhau hoặc đối nhau thì có giá trị tuyệt đối bằng nhau và ngược lại hai số có giá trị tuyệt đối bằng nhau thì chúng là hai số bằng nhau hoặc đối nhau.
|a| = |b| ↔ a = b hoặc a = -b
Mọi số đều lớn hơn hoặc bằng đối của giá trị tuyệt đối của nó và đồng thời nhỏ hơn hoặc bằng giá trị tuyệt đối của nó.
-|a| ≤ a ≤ |a| và -|a| = a ↔ a ≤ 0; a = |a| ↔ a ≥ 0
Trong hai số âm số nào nhỏ hơn thì có giá trị tuyệt đối lớn hơn. Nếu a |b|
Trong hai số dương số nào nhỏ hơn thì có giá trị tuyệt đối nhỏ hơn. Nếu 0 |a|2 = a2
Tổng hai giá trị tuyệt đối của hai số luôn lớn hơn hoặc bằng giá trị tuyệt đối của hai số, dấu bằng xảy ra khi và chỉ khi hai số cùng dấu.
|a| + |b| ≥ |a + b| và |a| + |b| = |a + b| ↔ ab ≥ 0
Tham khảo:
Phương trình chứa dấu giá trị tuyệt đối
Phương trình chứa dấu giá trị tuyệt đối là phương trình có chứa ẩn trong dấu giá trị tuyệt đối.
Xem thêm: Review Phim Những Đứa Con Của Gấu Mẹ Vĩ Đại, Những Đứa Con Của Gấu Mẹ Vĩ Đại
Phương trình có dạng: |f(x)| = a; (a>0)
Cách giải : |f(x)| = a;(a>0)⇔ f(x) = a hoặc f(x) = −a
Ví dụ: Giải phương trình |x + 1| = 2
Lời giải:
Phương trình có dạng : |f(x)| = |g(x)|
Cách giải : |f(x)| = |g(x)| ⇔ f(x) = g(x) hoặc f(x) = −g(x)
Ví dụ: Giải phương trình |x – 3| = |2 + 2x|
Bất phương trình chứa dấu giá trị tuyệt đối
Là bất phương trình có chứa ẩn trong dấu giá trị tuyệt đối. Thông thường, ta gặp ba dạng và sau đây là cách giải :
|f(x)| > g(x) ⇔ f(x) > g(x) hoặc f(x) |f(x)| 2 2|f(x)|
Các dạng bài toán liên quan đến giá trị tuyệt đối
Dạng 1: |A(x)| = k (Trong đó A(x) là biểu thức chứa x, k là một số cho trước)
Cách giải:
– Nếu k 0 thì ta có: |A(x)| = k → A(x) = k hoặc A(x) = -k
Ví dụ: Giải phương trình sau:
Dạng 2: Phương trình chứa dấu giá trị tuyệt đối dạng |P(x)| = |Q(x)|
Dạng 3: Rút gọn biểu thức và tính giá trị biểu thức
Phương pháp giải:
Với |a(x) + b + c| = d
Ta sẽ tính các giá trị bên trong giá trị tuyệt đối

Dạng 4: Đẳng thức chứa nhiều dấu giá trị tuyệt đối
Phương pháp giải:
Lập bảng xét điều kiện bỏ dấu giá trị tuyệt đối: |a(x)| + |b(x)| + |c(x)| = m
Căn cứ bảng trên xét từng khoảng giải bài toán (đối với từng điều kiện tương ứng)
Ví dụ Giải bất phương trình sau đây |2 – 5x| >= x + 1.
Sau khi đọc xong bài viết của chúng tôi các bạn có thể hiểu được giá trị tuyệt đối là gì, tính chất của giá trị tuyệt đối và các dạng bài tập giá trị tuyệt đối nhé